Causes & Effets • Dommage maximal et Date limite de maîtrise d’un risque

Par Guillaume Promé
le 17 Nov. 2020 • Risques et B/R, z. Blog-perso

Méthodes et techniques de prise en compte de la dynamique entre la cause d’un risque et ses effets, à des fins de maitrise.

Deux approches sont confrontées :

  1. Maitrise des risques en fonction de l’acceptabilité des effets courants ;
  2. Maitrise des risques en fonction des effets finaux acceptables.

La notion de date limite de maitrise est introduite.

Article largement nourri par une conférence d’Aurélien Crida, qui propose une réflexion autour des dynamiques exponentielles.

Modélisation

Des causes, puis des effets

L’analyse concerne des causes et des effets corrélés et potentiellement décalés dans le temps :

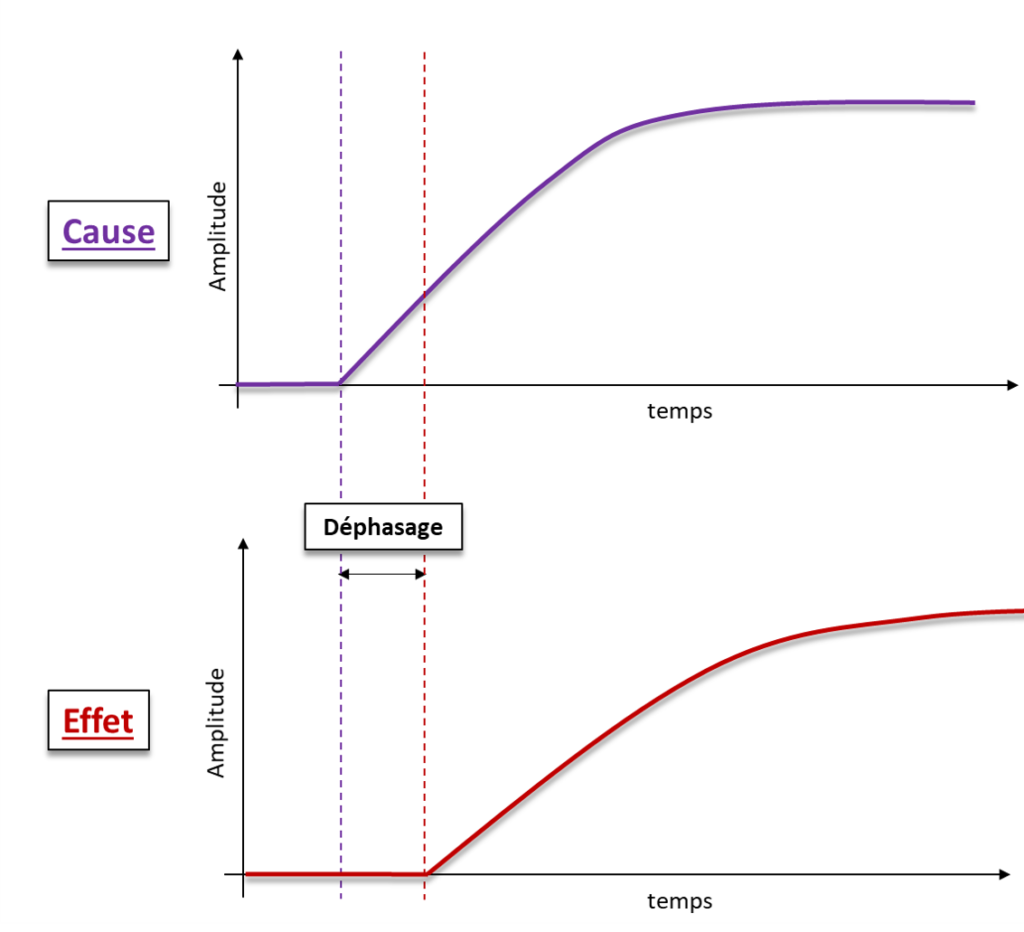
La maitrise n’est pas immédiate

  • La maitrise n’est pas immédiate : un délai effectif  s’écoule entre l’action de maitrise et des conséquences observables.
  • L’impact sur l’effet n’est pas immédiat : il débute après un temps de  déphasage entre cause et effet.

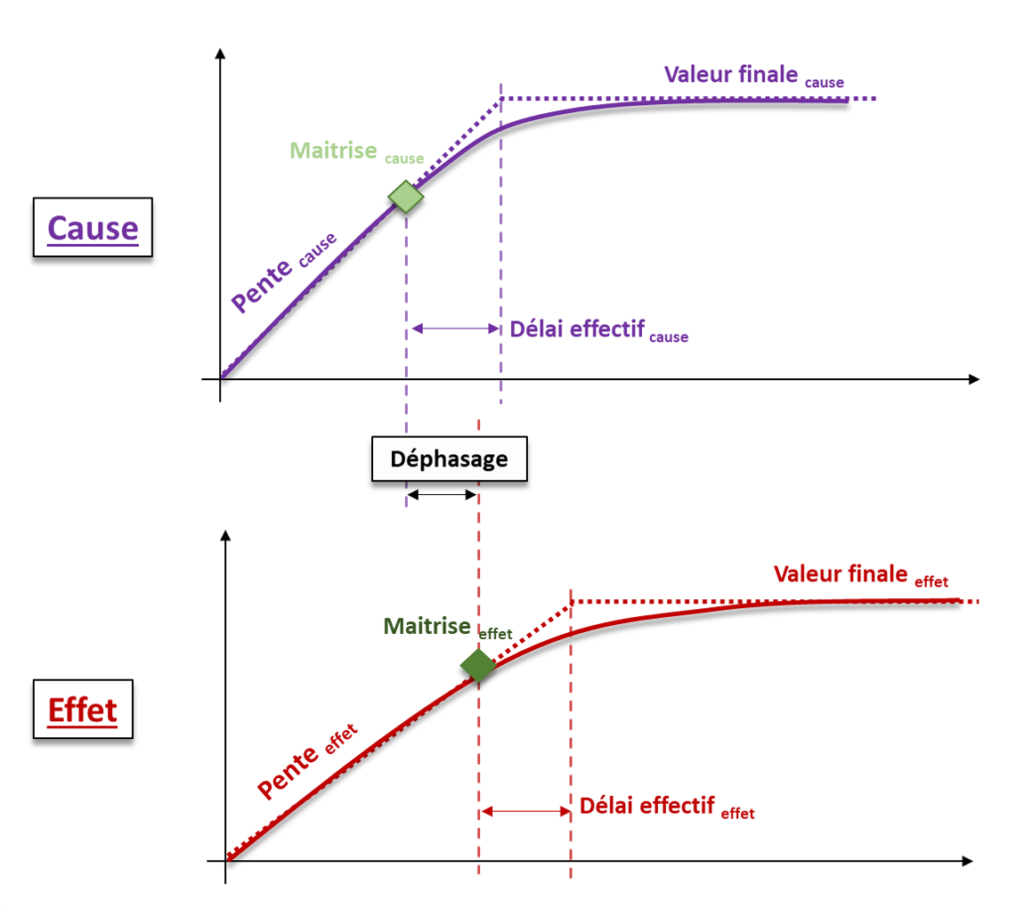
Les variables suivantes sont utilisées pour caractériser la dynamique d’une cause et d’un effet :

  • Pente avant maitrise ;
  • Instant de maitrise ;
  • Délai effectif de maitrise ; et
  • Valeur finale après maitrise.

Note :

  • Généralement le déphasage entre les maitrises est le même que celui entre cause et effet
  • Généralement les délais effectifs sont les mêmes entre causes et effets.
  • Souvent, les pentes sont les mêmes entre causes et effets.

Formules de base

Les formules dépendent de la dynamique, qui peut être linaire (c’est souvent le cas pour les analyses “micros“) ou exponentielle (c’est souvent le cas pour les analyses “macros“).

Dynamique linéaire

Pente_cause = d(cause)/dt
Pente_effet = d(effet)/dt
Valeur finale de la cause = Cause @Jmaitrise + pente_cause × delai effectif_cause

Dynamique exponentielle

Pente_cause = 1 – d(cause)/dt
Pente_effet = 1 – d(effet)/dt
Valeur finale de la cause = Cause @Jmaitrise × (1 + pente_cause)delais effectif_cause

Deux approches de la maitrise des risques

Deux approches sont possibles dans le cadre de la maitrise des risques :

  1. Réagir selon les effets courants ; ou
  2. Régir selon les effets finaux souhaités.

Approche par les effets courant

Principe

La décision de maitrise et déclenchée par un seuil sur les effets courants, la valeur finale de l’effet vaut alors :

En dynamique linéaire :

Valeur finale de l’effet = Effet @Jmaitrise × (1 + (dephasage + delai effectif_effet) × pente_effet)

En dynamique exponentielle :

Valeur finale de l’effet = Effet @Jmaitrise × (1 + pente_effet)(delais effectif_effet+déphasage)

Résultat

La valeur finale est un multiple de la valeur au jour de maitrise, en fonction du déphasage, du délai effectif et surtout de la dynamique.

La valeur finale peut être considérablement plus élevée que la valeur à l’instant de maitrise.

Cette méthode est déconseillée : elle peut mener à des effets finaux inacceptables.

Approche par les effets finaux souhaités : recours à une date limite de maitrise

Principe

La décision de maitrise et déclenchée par une valeur maximale acceptable des effets, la date limite de maitrise vaut alors :

En dynamique linéaire :

Date Limite de maitrise = Jcourant + (Effet_max_souhaité – Effet_courant)/pente_effet)

En dynamique exponentielle :

Date Limite de maitrise = Jcourant + log(Effet_max_souhaité/Effet_courant) – delais effectif_effet – dephasage_cause_effet

Résultat

La date limite de maitrise peut être extrêmement proche de la date courante, voire antérieure : ce qui rendrait la maitrise souhaitée impossible.

Cette méthode est conseillée : elle garantit des effets finaux acceptables.

Exemple avec la Covid-19 en France

La dynamique est ici exponentielle.

Cas et décès sont lissés sur sept jours. Les différences de pente entre première et seconde vague tiennent de la faible qualité des données disponibles en mars/avril et des mesures barrières mises en œuvre depuis.

Approche par les effets courants

C’est la méthode utilisée par le gouvernement.

Sur les graphiques : la valeur maximale de l’effet est calculée à partir de la date de maitrise.

Approche par les effets finaux souhaités

Il s’agit de définir un nombre de décès quotidiens acceptable et de maitriser (confiner) en fonction.

Le tableau ci-dessous reporte la Date Limite de Maitrise en fonction du pic quotidien de mortalité acceptable :

Décès/J max Date limite de maitrise
100 30 sept.
200 11 oct.
300 17 oct.
400 22 oct.
500 25 oct.
750 31 oct.
1 000 5 nov.
2 000 15 nov.

Conclusion

Raisonner selon les effets courants peut engendrer un risque final catastrophique, c’est particulièrement critique pour les dynamiques exponentielles qui s’emballent extrêmement rapidement.

Raisonner par date limite de maitrise permet une bonne maitrise des risques, mais conduit à des décisions de maitrise alors que les effets courants sont très faibles, ce qui nécessite un gros effort pédagogique pour être accepté.