Probabilités : estimations et suivi pour les dispositifs médicaux
Les probabilités sont utilisées par les fabricants de dispositifs médicaux pour l’analyse des risques (et des bénéfices) des dispositifs avant et après mise sur le marché. C’est une notion difficile à manier, qui peut conduire à des situations d’incompréhension voire à des erreurs de jugement.
Cet article présente un cadre théorique et des techniques pratiques pour travailler sur ces probabilités. .
Estimation des probabilités de risque (et de bénéfice)

Les probabilités sont dures à estimer, car elles varient de 100% à 1 chance sur plusieurs millions, jusqu’à être infiniment petites.
Les représentations chiffrées traduisent ce malaise : difficile de dire que 0,01% vaut 1/10 000 ou que 1/7 vaut 14%.
Choisir un référentiel
De fait, les probabilités doivent être estimées de façon “homogène”, c’est-à-dire dans un même référentiel.
On peut par exemple faire les estimations pour un dispositif, pour la durée d’exploitation par le fabricant, pour X mois, pour X patients… Il est conseillé d’estimer les probabilités pour une utilisation et pour un patient. Pour faciliter la comparaison des risques aux bénéfices (qui sont atteints par un patient, pour une utilisation).
Estimer un Niveau de probabilité
En première intention, et donc lors des premières analyses, les probabilités sont estimées “à la louche”, par niveaux.
Ici les niveaux de probabilité varient de 0 à 5, les chiffres négatifs exprimant des probabilités négligeables :
| Niveau de Probabilité | Description |
|---|---|
| 5 | Systématique |
| 4 | Très fréquent |
| 3 | Fréquent |
| 2 | Probable |
| 1 | Peu probable |
| 0 | Rare |
| -1 | Très rare |
Pratiquement, on pourra souvent estimer les probabilités en raisonnant par thème, par exemple en considérant la détectabilité du risque ou en prenant en compte les conditions nécessaires pour conduire au risque (conditions normales, anormales, exceptionnelles, inimaginables…).
Estimer des probabilités quantitatives
Les phénomènes qui ne relèvent pas du négligeable méritent des estimations précises, avec des probabilités quantitatives issues de vos données pré-cliniques, cliniques et de surveillance après commercialisation :
| Niveau de Probabilité | Description | Valeur |
|---|---|---|
| 5 | Systématique | 100% |
| 4 | Très fréquent | 10% |
| 3 | Fréquent | 1% |
| 2 | Probable | 1:1’000 |
| 1 | Peu probable | 1:10’000 |
| 0 | Rare | 1:100’000 |
| -1 | Très rare | 1:1’000’000 |
(Notez l’utilisation habile des pourcentages (%) et des taux (1:X), pour garder des représentations compréhensibles. Notez également la magie des maths :
ce qui permet, au besoin, d’aborder les probabilités avec des “niveaux de louches à virgules” et un bon tableur.)
Analyser les probabilités
Une ultime difficulté dans les estimations est due au fait que ce sont de nombreux événements qui conduisent à une situation donnée. Et il est plus facile d’estimer séparément les probabilités des événements conduisant au risque, que de tout estimer d’un coup.
Par exemple, on considérera :
- la probabilité d’avoir un dispositif qui fonctionne,
- la probabilité que l’utilisateur s’en serve correctement, et
- la probabilité que le patient réponde bien,
plutôt qu’imaginer directement la probabilité globale.
Dans tous les cas, la probabilité combinée est calculée à partir du produit des différentes probabilités :
Cela peut aussi être estimé avec une matrice, mais cette approche sera pénalisante lorsque de nombreuses probabilités entreront en jeux en jeu. Il vaut mieux une approche chiffrée, notamment pour l’analyse des situations possibles.
Réduire les probabilités des risques résiduels
C’est tout l’objet de votre maitrise des risques, qui permet aussi de réduire la gravité des dommages.
Il n’y a pas de consensus autour de l’impact des mesures de maitrise sur les probabilités d’occurrence des risques, cela varie de toute façon d’un dispositif à un autre, mais on retiendra que :
- La mise en œuvre de normes de sécurité ou de performance (essais en laboratoire notamment) permet de ramener les probabilités à des niveaux très faibles, de 1/10’000 à 1/1’000’000.
- Les moyens de maitrise “processus” (exemple : contrôles en fin de production) produisent des taux de non-conformité faibles, de l’ordre de 1/1’000 à 1/10’000.
- Les moyens de protection type alarme dépendent en partie du comportement de l’utilisateur avec des taux d’échec de l’ordre de 1%.
- Les maitrises par informations fournies (qui existent bel et bien, n’en déplaise à l’annexe Z de l’EN ISO 14971:2012) permettent difficilement de descendre en dessous des 10% de risque résiduel.
Probabilité des différentes situations possibles
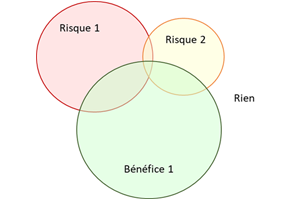
Combiner les risques 2 par 2 ne suffit pas pour cerner l’ensemble des situations possibles et pouvoir statuer sur l’acceptabilité des risques globaux. Il faut combiner TOUS les risques et bénéfices, en tenant toute fois compte de la vraisemblance des situations et de leurs probabilités (inutiles de prendre en compte des combinaisons d’événements qui ont chacun des probabilités très faibles).
Il est important de comprendre qu’un événement a deux facettes, avec deux probabilités : la probabilité P d’avoir l’événement et la probabilité 1 – P de ne pas avoir l’événement.
Ainsi, le cas simple d’un dispositif avec un seul bénéfice (PB=98%) et un seul risque (PR=0,1%) engendre quatre situations :
| Bénéfice uniquement
PB.(1-PR) = 97,9% |
Rien
(1-PB).(1-PR) = 0,02% |
| Bénéfice + Risque
PB.PR = 0,00098% |
Risque uniquement
(1-PB).PR = 0,00002% |
Un cas général de NR risques et NB bénéfices induit 2(NR+NB) combinaisons ! (64 pour 4 risques et 2 bénéfices, 4096 pour 10 risques et 2 bénéfices…).
Vous pouvez mener vos analyses en utilisant des tables combinatoires, exemple pour 1 bénéfice et 2 risques :
| Bénéfice (98%) | Risque 1 (0,1%) | Risque 2 (0,5%) | P |
|---|---|---|---|
| oui | oui | oui | 0,0005% |
| oui | oui | non | 0,098% |
| oui | non | oui | 0,49% |
| oui | non | non | 97,4% |
| non | oui | oui | 0,00001% |
| non | oui | non | 0,002% |
| non | non | oui | 0,01% |
| non | non | non | 1,99% |
(Notez que la somme des probabilités vaut bien 100% : tous les cas sont couverts).
Vous voilà avec énormément de situations possibles qui, selon la complexité de vos dossiers, seront impossibles à traiter à la main, il va falloir demander au service informatique une petite macro.
La plupart des situations ont des probabilités extrêmement basses qui sont négligeables pour l’évaluation de l’acceptabilité des risques d’un patient, mais elles deviennent significatives pour une population de patients, qui est exposée de multiples fois aux risques.
Probabilité d’exposition aux risques pour une population de patient
Sortir du “référentiel patient” propre à l’évaluation du rapport bénéfice/risque, et prendre en compte un ensemble de patients est une tache nécessaire pour les autorités et pour les fabricants (et leur assureur), qui ont une véritable population à gérer (les utilisateurs). La probabilité que le fabricant doive gérer un incident est souvent beaucoup plus grande que la probabilité pour un patient unique de subir un incident.
À ce stade une précision mathématique est nécessaire: une probabilité de risque de 10% ne veut pas dire que vous aurez un incident au 10ᵉ patient. En effet, la probabilité de ne jamais avoir le risque après N recours au dispositif vaut encore :
Ainsi, après 10 recours, vous avez 35% de chance de ne pas avoir eu d’occurrence d’un risque ayant une probabilité de P=10% (cette “chance” valait 90% au 1ᵉ recours).
Tout ceci permet de calculer le nombre de recours maximal à un dispositif, avant d’avoir K% de subir au moins une fois un risque de probabilité P (oui, ce n’est pas simple).
Exemple : vous voulez connaitre le nombre de recours au DM avant d’avoir K=90% de chance de subir au moins une fois un risque de probabilité P=0,1% :
Remarque : le cas “intuitif” où il faut X recours pour être exposé à un risque de probabilité 1/X (exemple : 1000 recours pour P=1/1000) équivaut à K=63%, soit 1 – 1/e, magie des maths.
Réestimation des probabilités après commercialisation
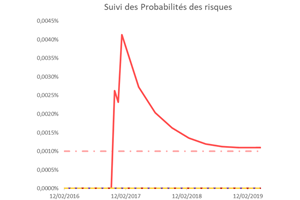
Cela fait partie de vos exigences en matière de surveillance après-commercialisation : définir des seuils et indicateurs pour gérer le rapport bénéfice/risque. L’idée est, notamment, de surveiller les probabilités d’occurrence des risques “clés”, les risques qui “pèsent” réellement sur votre rapport bénéfice/risque.
La probabilité d’un risque est réévaluée après commercialisation en tenant compte du nombre d’occurrence de l’incident Ni et du nombre total de recours aux dispositifs depuis la première mise sur le marché Nr
La difficulté est d’estimer Nr, en tenant compte du nombre de dispositif sur le marché, de leur durée de vie, du nombre de patient utilisant un même dispositif et de la fréquence de recours au DM (une seule fois, 1 fois par an, 2 fois par jour…).
Pour finir, il est important de mesurer la “maturité” des données d’après commercialisation, en comparant Nr avec le nombre total final Nf, fonction des ventes prévues pendant toute la durée de commercialisation :
Conclusion
Vous voilà armés pour estimer et suivre les probabilités de vos risques et bénéfices, le sujet n’est pas simple et nécessite une bonne méthode, pour aborder avec pragmatisme la gestion des risques, avec une approche basée sur les risques : ne pas trop en faire avec les risques de faible probabilité et gérer au mieux les risques de probabilité significative.

2 commentaires