Validation des procédés : Cp,Cpk, écart type… les méthodes statistiques
Lorsque les quantités produites sont suffisamment importantes, il peut être utile aux fabricants de valider la production, plutôt que d’effectuer des tests unitaires sur chaque dispositif.
Ces validations utilisent des outils mathématiques qu’il est nécessaire de comprendre pour les utiliser correctement.
Remarque : le sujet est traité dans la série de normes du comité ISO/TC 69/SC 4.
Définir les exigences sur la production
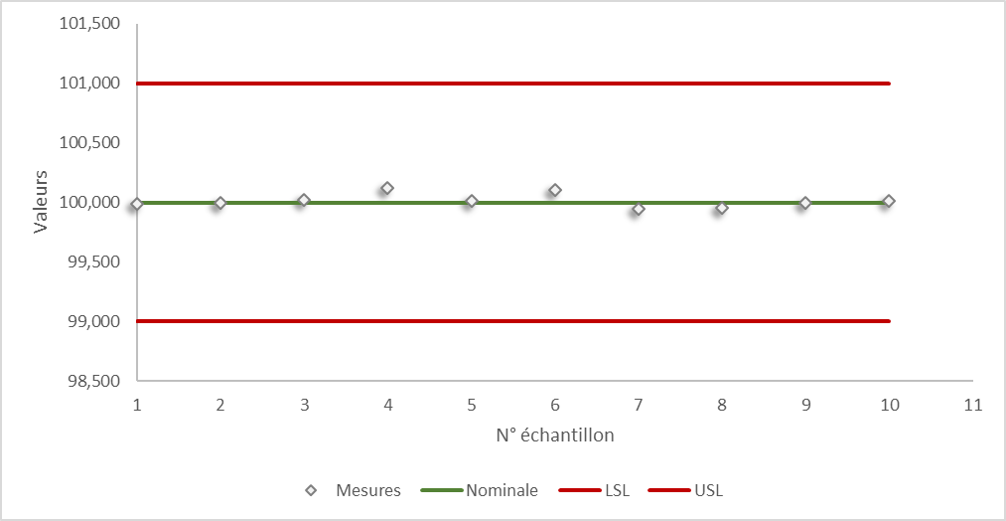
Avant de valider la production il faut définir des exigences sur les dispositifs fabriqués : ces exigences sont quantitatives, elles portent sur des caractéristiques physiques critiques du produit (exemple : une longueur, un diamètre, un taux…)
On fixe :
- Une valeur nominale (la valeur attendue) : X
- La tolérance haute : USL
- La tolérance basse : LSL
Ainsi, les pièces en dehors de la plage de tolérance seront non-conformes.
Distribution normale des valeurs mesurées
Pour plusieurs dispositifs fabriqués, une caractéristique mesurable va varier selon une distribution normale : la répartition des mesures (le nombre de pièce pour chaque plage de valeur) suit une courbe de gauss :
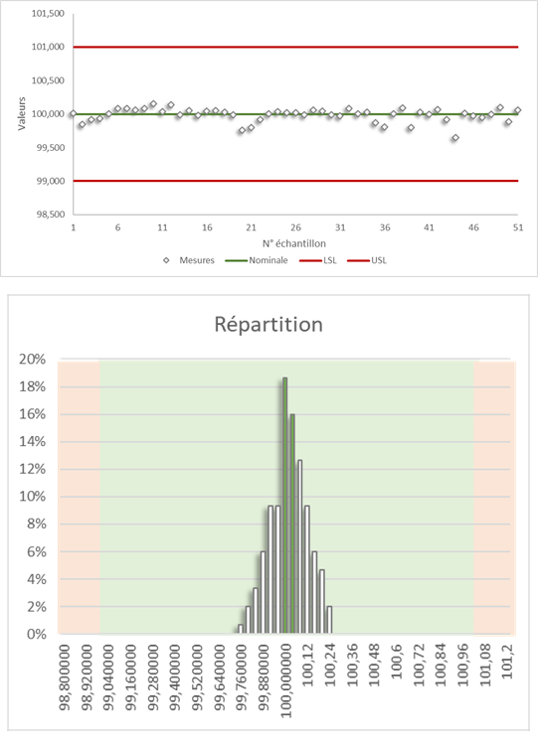
Dans cet exemple les 50 mesures permettent de tracer l’histogramme de répartition des valeurs, le fond vert couvre les valeurs conformes, les mesures NC sont en zone rouge. L’essentiel des points est proche de la valeur moyenne.
Plus la zone (rouge) de NC est éloignée de la courbe et plus le produit est susceptible d’être conforme
La validation de la production va démontrer que :
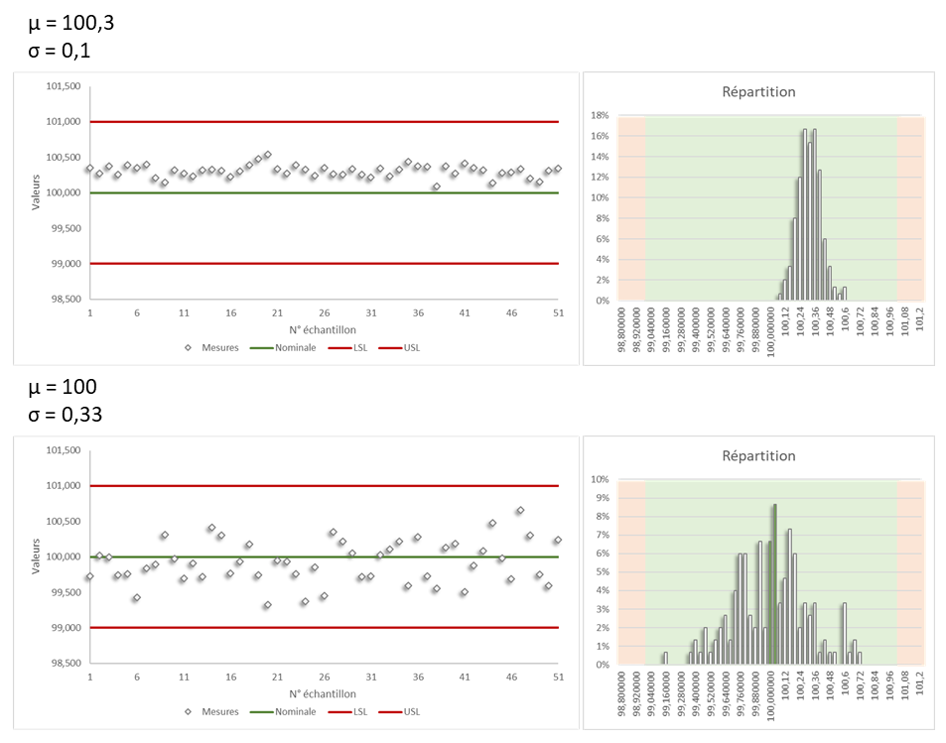
- la courbe est suffisamment étroite, pour ne pas dépasser de la zone de tolérance, la production est alors capable.
- la courbe est suffisamment centrée autour de la valeur nominale, pour ne pas sortir de la zone de conformité, la production est alors répétable.
Le centrage et la largeur de la courbe dépendent des réglages de l’outil de production et de ses éventuelles dérives.
Valeur moyenne et écart type des valeurs mesurées
Pour un lot de n pièces produites et les mesures x associées, on calcule :
- la valeur moyenne µ : Σ (mesures) / n
- l’écart type σ : √ ( Σ( ( x – µ)² ) / n )
La valeur moyenne est facile à comprendre (une valeur “au centre” de toutes les mesures), l’écart type est moins intuitif : il représente à quel point les mesures “partent dans tous les sens”.
Probabilité de non-conformité
C’est maintenant que l’outil mathématique se révèle utile : une fois la valeur moyenne et l’écart type identifiés il est possible de connaitre la probabilité d’un point d’être dans une plage de valeur donnée.
La probabilité P d’avoir une valeur dans un intervalle autour de la valeur moyenne est fonction du nombre d’écart types qui composent cet intervalle :
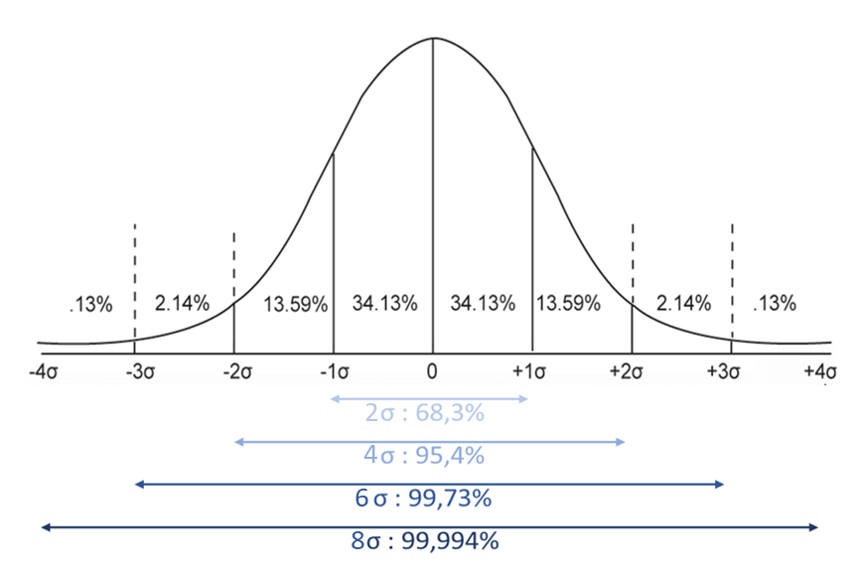
On en déduit la probabilité que la valeur soit en dehors de l’intervalle (que le produit soit non-conforme):
- x hors [-σ/2; σ/2] : 62%
- x [-σ; σ] : 32%
- x [-2σ; +2σ] : 5%
- x [-3σ; +3σ] : 0,27%
- x [-4σ; +4σ] : 0,006%
- x [-6σ; +6σ] : 0,0000002%
Le but est d’avoir des tolérances (USL et LSL) très éloignées de la valeur moyenne, typiquement de 4σ chacune : avec une probabilité de conformité de 99,994% et un taux de non-conformité de 66ppm (pièces par million).
Coefficients de capacité Cp, Cpk, Cpm
Calculs
Des indices sont nécessaires pour analyser les résultats de production :
- Indice de capacité du procédé : Cp = (USL – LSL) / 6σ
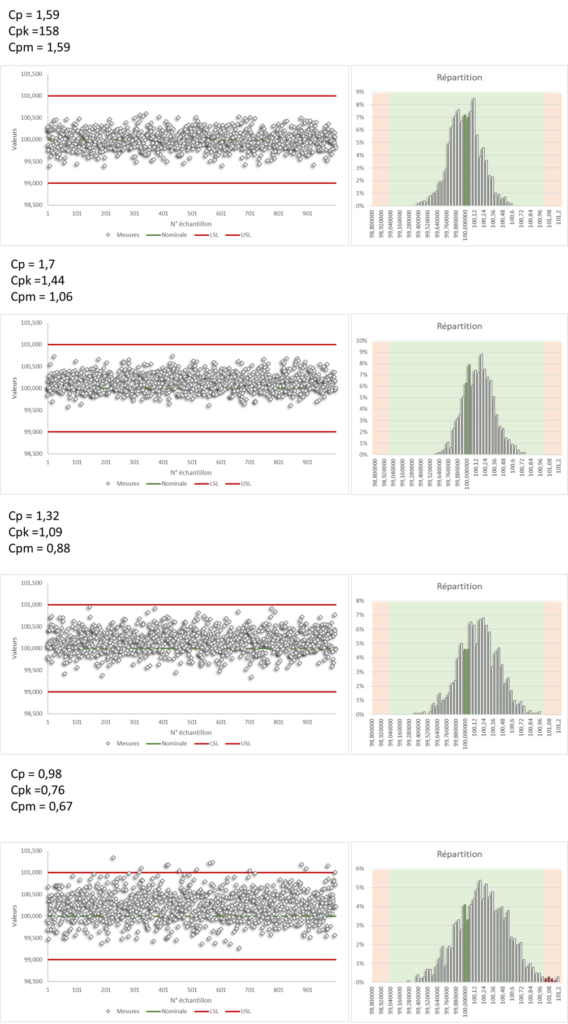
Le coefficient Cp regarde “à quel point la plage de tolérance est proche de 6σ” : plus Cp est grand et plus votre procédé est capable de produire des résultats conformes.
Avec Cp = 1 la plage de conformité couvre 6σ, la probabilité d’être non-conforme est de 0,27%
Avec Cp = 1,33 la plage de conformité couvre 8σ, la probabilité d’être non-conforme est de 0,007%
- Indice de capacité minimal du procédé Cpk = min( (USL – µ)/3σ ; (µ – LSL)/3σ)
Le coefficient Cpk tient compte d’un éventuel décentrage, qui malgré un Cp élevé rendrait le procédé peu répétable
- Indice de capacité machine : Cpm = Cp / √( 1 + 9.(Cp – Cpk)²)
Le coefficient Cpm (très utile car très réactif) tient compte du décentrage des résultats, il est couramment utilisé pour surveiller le déréglage d’une machine.
Seuils utiles
Les seuils, permettant de statuer si les coefficients Cp, Cpk et Cpm sont satisfaisants, dépendent de la confiance souhaitée :
Les seuils courants et les probabilités de confiance associées sont données ci-dessous, un seuil de 1,33 est très souvent utilisé, 1,66 relève des productions d’excellence (nécessaire pour de grandes quantités de pièces).
| Seuil | Sigmas (score z) | confiance | NC |
|---|---|---|---|
| 0,67 | 2,01 | 95,56% | 44’431ppm |
| 1 | 3 | 99,73% | 2’700ppm |
| 1,33 | 3,99 | 99,9934% | 66ppm |
| 1,66 | 4,98 | 99,999936% | 1ppm |
| 2 | 6 | 99,9999998% | 0ppm |
On note le “score z” : z = 3.S
Nombres d’échantillons utilisés et erreur induite
On peut calculer l’erreur e en fonction de σ, du nombre d’échantillons n et de z :
e = z.σ/√n
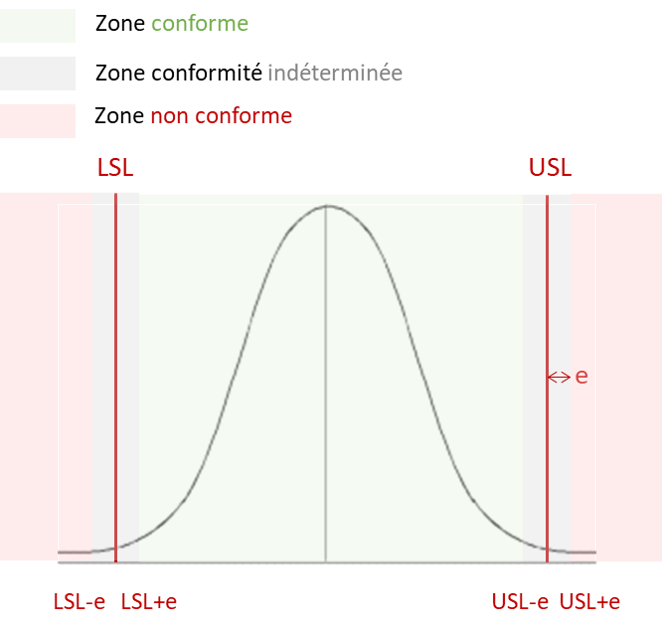
L’erreur va réduire la plage de conformité, en effet : autour des valeurs LSL +/- e et USL +/-1 vous ne savez pas si la mesure est conforme.
Vous avez maintenant trois zones : conforme, non conforme et inconnu :
Comment utiliser tout ça ?
Pour chaque essai de validation (il y a souvent un essai par facteurs d’influence et cycle de production) :
- Faire quelques dizaines de prélèvements (classiquement plus de 20)
- Calculer les coefficients Cp, Cpk, Cm et l’erreur
- Continuer jusqu’à avoir des coefficients stables puis une erreur tolérable
Vous tiendrez compte du nombre de dispositifs produits pour fixer un seuil pour les indices de capabilité. Un seuil élevé – supérieur à 1,3 – serra nécessaire pour de grosses productions où même les faibles probabilités de non-conformité sont critiques.
Le nombre de prélèvements requis va de quelques dizaines à plusieurs centaines en fonction de l’écart type et de vos volumes de production.
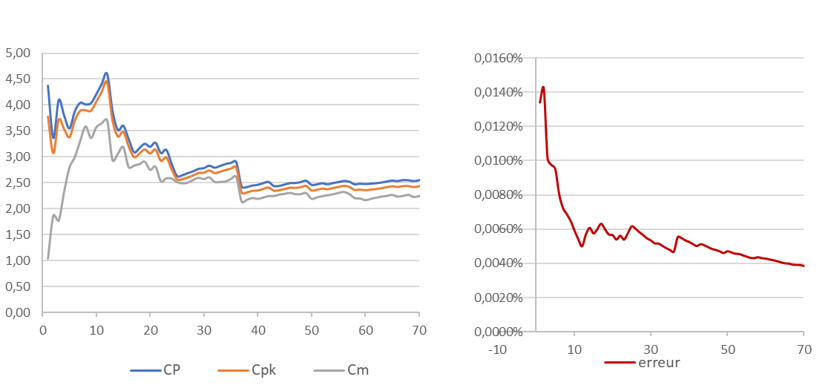
Ci-dessous : l’évolution de l’estimation des coefficients et de l’erreur en fonction du nombre d’échantillons, pour un écart type faible (moins d’1/5 de la tolérance), on constate que les valeurs sont correctement estimées après une quarantaine d’échantillons :
Feuille de calcul
Lien vers la Feuille de calcul utilisée pour illustrer le présent article.

13 commentaires